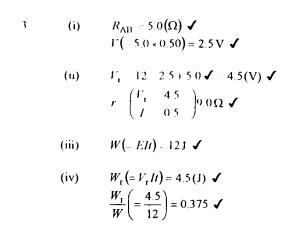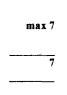PH01 Summer 2000

 

1.  A machine gun fires bullets of mass 0.050 kg at a speed of 450 m s^-1

     (a)   Calculate the momentum of a bullet as it emerges from the gun.                            (2)

     (b)   (i)     Explain why a soldier holding the machine gun will experience a force from the gun whilst it is firing bullets.

            (ii)    The maximum steady horizontal force a soldier can exert on the gun is 150N. Calculate the maximum number of bullets the gun can fire every second.                                            (4)= (6)

 

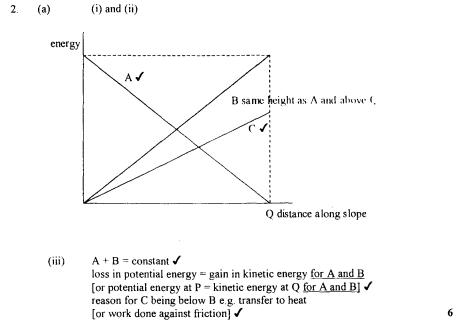
2   (a)   The diagram shows an object at rest at the top of a straight slope which makes a fixed angle with the horizontal.

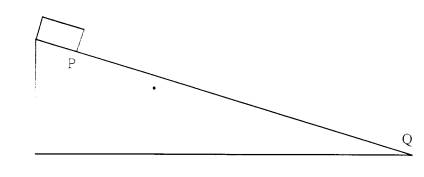
     (i)    The object is released and slides down the slope from P to Q with negligible friction.

            Assume that the potential energy is zero at Q. Sketch a graph showing the potential energy at different distances measured along the slope, and label it A. On the same set of axes, sketch a second graph showing the kinetic energy of the object at different along the slope and label it B.

Energy

     (ii)    Using the same axes as in part (1), sketch a third graph, labelled C, showing the kinetic energy at different distances along the slope when there is a constant frictional force between the object and the surface.

     (iii)   Use  your knowledge of the principle of conservation of energy to explain the important features of the graphs you have drawn in part (i) and part (ii).

 

3   A battery of e.m.f. 12 V and internal resistance r is connected in a circuit with three resistors each having a resistance of 10 ohms as shown. A current of 0.50A flows through the battery

.

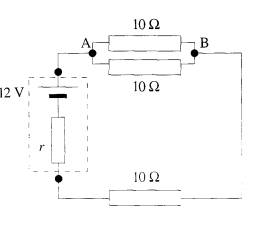
Calculate

(i)    the potential difference between the points A and B in the circuit,
(ii)    the internal resistance of the battery,
(iii)   the total energy supplied by the battery in 2.0 s,
(iv)   the fraction of the energy supplied by the battery that is dissipated within the battery.

 4   A filament lamp rated 12 V  1.0 A has a resistance of 4.0 ohms when it carries no current.

     (a)   On the axes below. sketch the form of the current against voltage characteristic for this lamp.

(4)

     (b)   The filament lamp is one example of a non-ohmic device.

            (i)     State what is meant by the term non-ohmic.

       (ii)         Name one other example of a non-ohmic device.                                                (2)=(6)

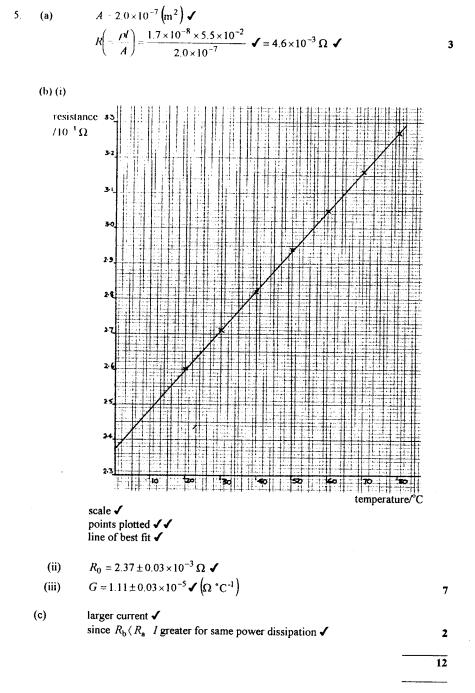
5    (a)    A 15 A fuse uses a 55 mm length of copper w ire of diameter Calculate the resistance of the copper wire at 20 oC.

 

resistivity  of copper at 20 °C = 1.7 x 10 -8 ohm m

 

        (b)  Another copper fuse with a different current rating, has a resistance of 2.60 x 10-3 ohm at 20 °C. Its resistance increases with temperature as shown in the table.

 

 

      (i)           Plot a graph of resistance, R, against temperature. theta on the axes provided

      (ii)                   Use your graph to determine the resistance of the fuse at 0 -C.

      (iii)         Determine the gradient of the graph.

 

      (c)        The fuse in part (b) has the same length as the 15 A fuse in part (a). Explain whether the fuse in part (b) is designed for a current which is larger or smaller than the 15 A fuse.

(7)=(12)

 

 

6    One end of a steel wire of length 1.2m and 2.0 mm diameter is attached to a rigid beam.

A 25 g mass is attached to the free end of the steel wire and placed against the underside of the beam as shown.

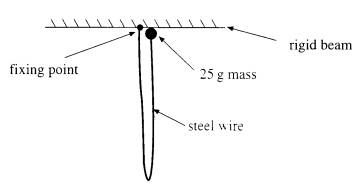
The 259 mass is released and falls freely until the wire becomes taut. The kinetic energy of the falling mass is converted to elastic potential energy in he wire as the wire extends to a maximum of 1.0 mm. Energy converted to other forms is negligible.

 

For maximum extension of the wire, complete parts (i) to (v)

(i)     Show that the elastic potential energy stored by the wire is 0.29J.

(ii)      Calculate the tension in the wire.

(iii) Calculate the stress in the wire.

(iv) Calculate the strain of the wire.

(v)      Hence, calculate the Young modulus for the steel of the wire

(9)=(9)

 

 

PH01 March 2000

 

       A cyclist rides along a road up an incline at a steady speed of 9.0 m s^-1 The mass of the rider and bicycle is 70 kg and the bicycle travels 15 m along the road for every 1.0 m gained in height. Neglect energy loss due to frictional forces.

(a)    (i)         Calculate the component of the weight of the bicycle and the rider that acts along the incline.

       (ii)         Calculate the power developed by the cyclist in riding up the slope.                                      (4)

(b)    The cyclist stops pedalling and the bicycle freewheels up the incline for a short time.

       (i)         State the energy change taking place as the bicycle freewheels up the slope.

       (ii)      Calculate the distance travelled along the slope from when the cyclist stops pedalling to where the bicycle comes to rest.                                                                                                    (3)

 

2    The Thrust SSC car raised the world land speed record in 1997. The mass of the car was 1.0 x 10⁴ kg. A 12 s run by the car may be considered in two stages of constant acceleration. Stage one was from 0 to 4.0 s and stage two 4.0 s to 12 s.

      (i)     In stage one the car accelerates from rest to 44 m s^-1  in 4.0s. Calculate the acceleration produced and the force required to accelerate the car.

      (ii)    In stage two the car continue to accelerate so that it reached 280ms-1 in a further 8.0s.   Calculate  the acceleration  of the car during stage two.

      (iii) Calculate the distance travelled by the car from rest to reach a speed of 280ms-1

 

3      (a)      State the principle of moments.

       (b)      (i)       A uniform plank of length 1.5 m and mass 9.0 kg is placed horizontally on two narrow vertical supports as shown. A block, X, of mass 3.0 kg is placed at the end of the plank immediately above the centre of the right-hand support.

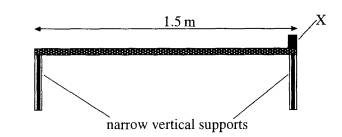
Calculate the magnitude of the downward force on

·    the right-hand support

·    the left-hand support

(ii)      The block X is now moved so that its centre of mass is immediately above a point 1.0 m from the right hand edge of the plank.

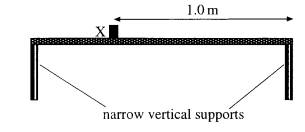
Calculate  the magnitude of the downward force on:

·         the right-hand support.

·         the left-hand support                                                                                                             (6) =(8)

5. In the circuit, the battery has negligible internal resistance and voltmeters V, and V₂ are of very high resistance. Voltmeter V, shows a reading of 0.65 V.

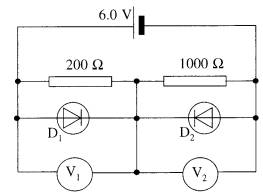
(i)         State whether each of the diodes is conducting.

(ii)         What is the reading shown on voltmeter V2?

(iii)        Calculate   the current flowing through the 1000 ohm resistance. (iv) Calculate the current flowing through D1.                                                                                                                        (7) (7)

 

6   (a)   Write down an equation relating the electrical resistivity of a material to the resistance of a particular sample. Define the symbols used.                                                                                                   (2)

     (b)   (i)     A cylindrical sample of graphite 10 mm long and with diameter 6.0 mm has a resistance of 450 ohm.

                   Calculate  the electrical resistivity of graphite.

            (ii)    Calculate   the resistance of a specimen of copper of the same dimensions as that of the graphite specimen in part (b)(i).                                                                                              (5)

 

PH01 Summer 1999

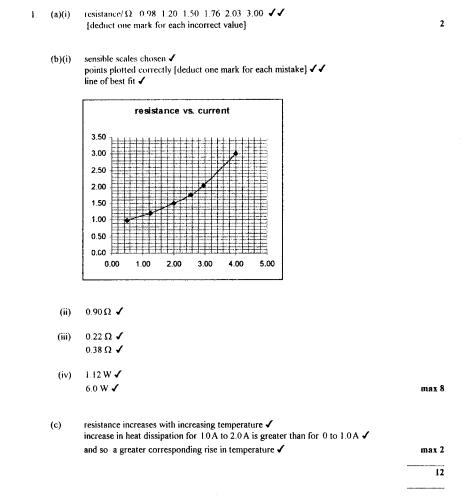
1      In an attempt to investigate how the resistance of a filament lamp varies with current through the lamp, a student obtains the results shown in the table.

     (a)   Complete the table by calculating the corresponding values of resistance.  
                                                                                                    (2)

     (b)   (i)     On the grid opposite plot a graph of resistance against current for the filament lamp.

            (ii)    Use your graph to estimate the resistance of the filament lamp when no current flow s through the lamp.

            (iii)   Use your graph to determine the change in the resistance of the filament when the current increases from

•   0 to 1.0 A

•   and from 1.0 A to 2.0 A      

            (iv)   Calculate the power dissipated in the lamp filament when the current through the filament is 1.0 A and 2.0 A.

(8)

     (c)   Using information from part (b)(iv), explain why the change in resistance of the filament is less for a current change of 0 to 1.0 A than for a current change of 1.0 A to 2.0 A. Do not attempt any calculation.

(2)=(12)

2   (a)   Show that the unit of resistivity is ohm m.

     (b)   A cable consists of seven straight strands of copper wire each of diameter 1.35 mm as shown in the diagram.

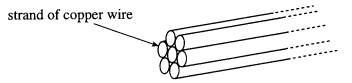
            Calculate

            (i)     the cross-sectional area of one strand of copper wire,

            (ii)    the resistance of a 100 m length of the cable, given that the resistivity of copper is 1.6 x 10^-8 ohm m.

.    (4)

     (c)   (i)     If the cable in part (b) carries a current of 20 A, what is the potential difference between the ends of the cable?

            (ii)    If a single strand of the copper wire in part (b) carried a current of 20 A, what would be the potential difference between its ends?

(2)

     (d)   State one advantage of using a stranded rather than a solid core cable with copper of the same total cross-sectional area.

 (1)=(8)

4   (a)   (i)     Give an equation showing how the principle of conservation of momentum applies the colliding snooker balls shown in the diagram

            (ii)    State the condition under which the principle of conservation of momentum applies.

(3)

    (b)  A trolley, A, of mass 0.25 kg and a second trolley, B of mass 0.52 kg are held in contact on a smooth horizontal surface. A compressed spring inside one of the trolleys is released and they then move apart. The speed of A is = 2.2 ms^-1

         (i)   Calculate the speed of B.

         (ii)  Calculate a minimum value for the energy stored in the spring when compressed.

(4)

     (c)   The rotor blades of a helicopter sweep out a cross-sectional area, A. The motion of the blades helps the helicopter to hover by giving a downward velocity, v, to a cylinder of air, density p. The cylinder of air has the same cross-sectional area as that swept out by the rotor blades.

            Explaining your reasoning:

            (i)     derive an expression for the mass of air flowing downwards per second, and

            (ii)    derive an expression for the momentum given per second to this air.

            (iii)   Hence show that the motion of the air results in an upward force, F, on the helicopter given by

(5)

     (d)   A loaded helicopter has a mass of 2500 kg. The area swept out by its rotor blades is 180 m². If the downward flow of air supports 50% of the weight of the helicopter, what speed must be given to the air by the motion of the rotor blades when the helicopter is hovering? Take the density of air to be 1.3 kg m ³.

(3)=(15)

(4)